今天，新航道天津学校小编给大家带来的是GRE数学真题解析，专业的天津GRE培训机构就选新航道天津学校，想了解新航道GRE课程的可以到新航道天津学校进行免费评估，由专业的老师为您定制专属GRE备考计划。

在9月GRE数学改革后，虽然考点没有变化，每次考试还是从150个考点中，随机抽取27道题（涉及30个左右考点）考察大家的掌握情况，但是具体考查形式还是在不断推陈出新~ 比如，近期很多同学被以下这道GRE数学题唬住了~

而且，这种考法并不是孤立的，类似的考题还有——

或者还有看起来更复杂一点的形式，比如下面这道题——

到底这些题在考什么？

考场第 一次遇到这类题的童鞋们肯定都懵了，啥呀这是？不怕，今天就带大家一次性弄清楚这类题的解题技巧~

首先，让我们迅速回顾一下本题相关的考点，系统学习一下相关的解题技巧——

一、知识点复盘

【相关考点】

6.3.1计数原理

【不同考查角度】

考察角度一：枚举法（本题相关）
1）针对问题：无典型规律的计数统计题
2）典型情境：总可能性有限
3）计数公式：仔细列举，耐心统计，求和即为总可能性

考察角度二：极限法
1）针对问题：简单计数统计题
2）典型情境：做一件事，有不同的几种方法，但是可能取值是连续的
3）计数公式：省去列举，找到取值b与最小取值a，总可能性b-a+1

考察角度三：加法原理
1）针对问题：条件笼统宽泛，分情况讨论问题
2）标志词：at least, no more than……
3）典型情境：做一件事，完成它需要分成n种不同情况，第 一种情况有m1种不同的方法，第二种情况有m2种不同的方法，……，第n种情况有mn种不同的方法。
4）计数公式：完成这件事共有 N=m1+m2+m3+……+mn 种不同的方法

考察角度四：乘法原理
1）针对问题：条件明确，分步骤问题
2）标志词：first, then……
3）典型情境：做一件事，完成它需要分成n个步骤，做第 一步有m1种不同的方法，做第二步有m2种不同的方法，……，做第n步有mn种不同的方法。
4）计数公式：完成这件事共有 N=m1×m2×m3×&……×mn 种不同的方法

考察角度五：乘法原理&加法原理复合
1）针对问题：分类&分步复合问题
2）典型情境：在题目条件下，既需要分类，又需要在每类情况下，分步统计可能性
3）计数公式：总体分类求和，内部分步求积

考察角度六：乘法原理&倒减思维
1）典型情境：分步相乘求积，统计总可能性的前提下，题目明确要求排除个别几种可能性
2）计数公式：每个步骤的可能性相乘求积之后，减去不需要的可能性

考察角度七：乘法原理&反算思维
1）针对问题：复合分类问题
2）典型情境：情境较多，或者正向统计较为麻烦耽误时间的情况下，累加求和较为繁琐，为了提高解题速度，可以主动反算
3）标志词：at least one
4）计数公式：总可能性-反向可能性

考察角度八：乘法原理&涂色问题
1）典型情境：乘法原理的情境下，步骤与步骤之间，相互需要满足一定的限制与照应关系
2）计数公式：仔细分析在充分照应题目条件限制下，每进行下一步的可能性，然后再将不同步骤的可能性乘起来

二、现学现用

知道相关概念后，我们再回到第 一题：

相对而言，其他方法虽然也许也能够解出来本题（比如标数法），但是相较枚举法，反而有点大炮打苍蝇的感觉，反而更为麻烦容易出错。，不太适合GRE数学考场上使用。

本题出现在近期GRE数学考试Section 自适应Hard第08题的位置！

现阶段，GRE数学考试遇到类似题，还是推荐大家先跳过不做！

等其他题都做完，再Review跳回来，有耐心直接枚举即可！

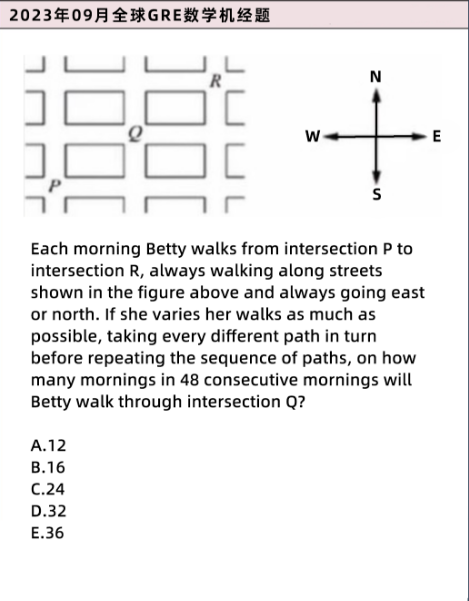
从上到下，逐个拐点仔细辨别，不要遗漏可能性即可——
01258
012438
01243678
0138
013678
因此，一共有五种不同走法，答案选C即可。

举一反三

类似地，大家也可以试着求解另外两道同考点题试试！
千万不要嫌麻烦，灵活调整做题节奏，最后跳回这类题仔细列举即可~

>>相关考题一：

【过往命中时间】2023年09月15日中国线上；2023年03月24日北美线上；2023年01月29日北美线上；2022年11月04日中国线上；2022年09月05日中国线上；2022年03月01日中国线上；2022年01月06日中国线上；2021年11月24日 北美线上；2020年09月25日中国线上；2020年07月30日北美地区线上

【参考答案】选C

【参考解析】

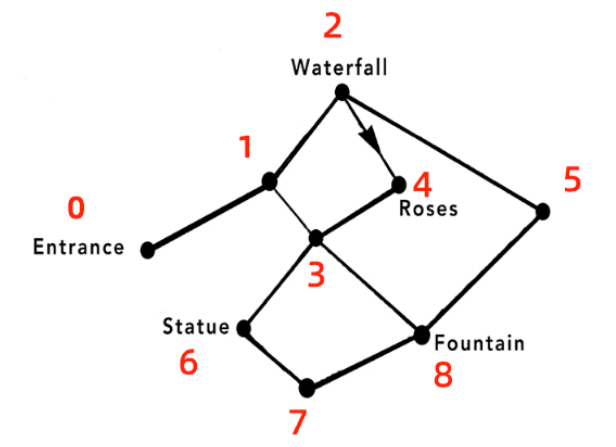
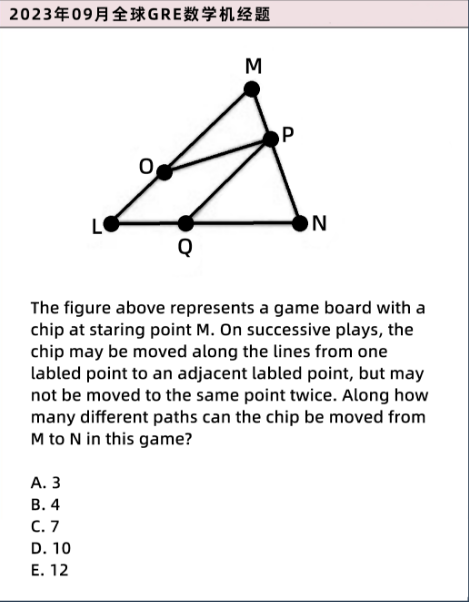
枚举满足要求的路径包含——
MPN 
MPQN 
MPOLQN 
MOPN 
MOPQN 
MOLQPN 
MOLQN 
一共有7种不同的走法 
【参考难度】3 
【相关考点】6.3.1 计数原理

>>相关考题二：

【过往命中时间】2023年09月15日中国线下；2023年07月13日中国线上；2022年11月17日中国线上；2022年08月03日北美线下；2022年01月11日北美地区线上；2021年09月10日北美地区线上；2020年12月13日中国线下
【参考答案】选D 
【参考解析】 
方法一：由于走的方向有限，预判可能性不会很多，可以适当枚举——

东东北北
东北Q北东 
东北Q东北 
北东Q东北 
北东Q北东 
北北东东 
总共6种走法，其中4种经过Q，经过概率4/6，经过次数48*(4/6)=32 

方法二： 如果实在觉得列举麻烦，可以尝试按照下方思路做——
由题可知，沿田字型的路线从P往R走，且只能向右或向上走，共分4步完成，其中有2步向右，有2步向上，故主动构建组合模型，四个步骤里，随意选择2个步骤，往上走，剩余两步自然往右走，因此所有的走法共有C（4,2）*C（2,2）=6种方法． 其中经过点Q的走法有2×2=4种，故经过点Q的概率是4/6=2/3。 总共走48次，2/3的概率通过Q，所以48*(2/3)=32次通过Q 
【参考难度】4 
【相关考点】6.3.1 计数原理 & 6.4.1 古典概率

以上就是新航道天津学校小编给大家带来的今天GRE数学真题解析，专业的天津GRE培训机构就选新航道天津学校，新航道天津学校为学生提供雅思、托福、A-Level、AP等各类出国考试培训、英语学习、留学咨询、背景提升等服务。

新航道天津学校为您提供......

      新航道天津学校-作为17年的雅思|托福|sat培训辅导机构，为您提供雅思培训课程、托福培训课程、sat培训课程，雅思、托福、sat报考、考试、备考资料、查分等信息。同时还为您提供雅思考试流程，雅思培训服务，并提供雅思备考专区；更多的雅思口语、雅思听力、雅思写作、雅思词汇、雅思阅读、天津雅思培训相关信息为您提供，圆你出国留学梦想。